概览

KMP算法是一种字符串匹配算法，用于在一个字符串（称为目标字符串）中查找一个子串（称为查找字符串）的出现位置 比如说在目标字符串 ababceabcde 中查找一个字串 abcd 的出现位置，返回下标，如果没有出现就返回 -1。其实就是很多语言都有的 indexOf 的实现

在本文的讨论中都会使用该目标字符串**(S代指)** ababceabcde 和查找字符串**(P代指)** abcd

滑动窗口

最直接的实现是逐字比较，目标字符串和查找字符串诸位比较，如果某一位匹配不上就从目标字符串的下一位重新开始匹配：

file

file

file

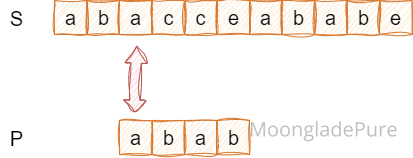
直到匹配完成或者匹配不上为止：

file

这个方法的时间复杂度为 O(mn)，m 为目标字符串的长度，n 为查找字符串的长度

然而有一个 KMP 算法能够达到 O(m+n) 的时间复杂度！

KMP 算法

简单的说 KMP 算法是通过跳过重复的字符来提升查找效率，图示如下： 从 S（目标字符串，下文都用 S 指代） 和 P（查找字符串，下文都用 P 指代）的第一个字符（下标 0 ）开始匹配，匹配到 S 的下标 3，和 P 的下标 3，双方的字符不匹配：

file

这个时候重点来了！此时正在匹配的 S 的字符是 S[3]，该下标不变，直接将 S[3] 的字符和 P[1] 继续比较，（为什么是 P[1] 而不是 p[0] ？这是个最关键的问题，我们马上会讲到）

file

继续往下匹配，匹配失败，那么 S[3] 下标不变，P 从下标 0 开始匹配

file

S[3] 和 P[0] 字符匹配失败，从 S 的下一个下标开始匹配，即 S[4] 匹配 P[0]，直到有一个字符匹配成功：

file

S[6] 和 P[0] 匹配成功，则两边都继续匹配下一个字符，即 S[7] 和 P[1]

此时逐字匹配成功，返回下标 6

file

那么问题来了，当 S[i] 和 P[j] 的字符匹配失败的时候，我怎么知道要从 P 的哪里重新开始匹配呢？这就涉及到一个 KMP 中最重要的概念：next 数组

next 数组

next 数组就是为了解决上述问题，当 S[i] 与 P[j] 匹配失败的时候，next[j] 返回的 k 就会告诉 P，如果如果你的下标 j 的字符不匹配，那么应该从下标 k 开始匹配，即从 P[k] 开始继续匹配

此时 S 的下标是不变的，所以下一次匹配的字符是：S[i] 和 P[k]

为了进一步理解 next 数组的作用，看下面图示：

file

S[2] 和 P[2] 匹配失败，将 P 当前匹配失败的下标 2 所为索引，从 next 中取出下标为 2 的数据，为 1，表明下次匹配应该从 S[2] 和 P[1] 开始。

file

file

直到匹配成功或者失败

在开始构建 next 数组前一定要先明白 next 数组的作用和使用方式：

  1. next 数组让 P 中重复出现的字符跳过匹配，
  2. next 数组的下标表示 P 的下标所代表的字符
  3. next 数组的下标 i 的值 k，表示 P 中该下标 i 的值如果匹配失败，下次要从 k 下标开始匹配

如：下图的 S[3] 和 P[3] 匹配失败，经过了 next 数组，下一次直接从 S[3] 和 P[1] 匹配，在下面的图例中能看到 S[2] 和 P[0] 是匹配的，但是我们直接跳过 S[2] 和 P[0] 匹配过程！

file

file

S 的下标从来没有往后退过一格。

那么如何构建 next 数组？

构建 next 数组

最长相同前后缀子串

在这之前要先理解一个概念：最长相同前后缀子串，也就是一个字符串中前缀和后缀相同的部分，比如 abcmmcabc 中，前缀部分 abc 和后缀部分 abc 是相同的，那么他们的相同前后缀子串就是 abc，长度为 3。

但是前缀 a 和 后缀 a，ab 和 ab 也是相同前后缀子串啊，没错，但是我们要的是最长相同前后缀子串，所以在上面中只能是 abc。

最长相同前后缀子串 将对跳过重复字符起到关键作用！如有以下查找字符串：abcmcabcp，如果此时我已经匹配到了下标 8 了，如下图：

file

那么下次匹配应该要从 P 的开头跳过尽可能多的、与 S 已经匹配过的相同字符，在上图中我们能够看到，在 S 中已经和 P 匹配成功的部分：abcmcabc，S 的后缀 abc 与 P 的前缀 abc 相等，且是最长相同前后缀子串，长度为 3，那么 P 的前三个字符就可以跳过下次的匹配，直接让 P 的第四个字符来匹配，来和这一次没有匹配成功的 S 的字符匹配。

这句话有点绕，要多读几遍。

file

如上图的流程，就是最长相同前后缀子串的作用。

而在 next 数组中，next[i] 就记录了 P[0..i] 的最长相同前后缀子串的长度。

构建最长相同前后缀子串

就像上一段举的例子里说的，前后缀子串是指 P 的前缀和 S 的已经匹配成功部分的后缀，但是因为 S 中和 P 匹配成功的部分，正好和 P 的一部分是一样的

file

如图上，S 中和 P 匹配成功的部分 S[*..i] == P[0..j] （这里 S[*..i] 是代指可能为任何下标 * <= i），这两个串完全相同，所以当我们求 P[0..j] 的前缀和 S[*..i] 的后缀最长的相同子串的长度，可以简化为求 P[0..j] （0 <= j < P.length）本身的最长相同前后缀子串长度，因为 S[*..i] 和 P[0..j] 是完全相同的！

首先说明：next[0] 的值一定为 0，因为 P[0] 已经是第一个字符了，就算 P[0] 字符不匹配下次也只能从 P[0] 开始匹配，所以 next{0] 只能为 0

接下来求 next 数组其他位置的值 定义两个下标指针 l，r，l=0，r=1

let l = 0;
let r = 1;

因为 next[0] 为 0，下一个是求 next[1] 的值，也就是 P[0..2] 的最长相同前后缀子串的长度。那么只要将 P[0] 和 P[1] 作比较，如果相同，说明两者的相同字符子串长度可以 +1 了，然后比较两个子串的下一个字符：l++，r++。

如果 P[0] 和 P[1] 不相等的，那么说明 P[0..2] 的最长相同前后缀子串的长度为 0，next[1] 的值应该为 0，这种情况下，将 r++，l 不变。但其实这句话的描述并不能很好地说明为什么要这么做，要抽象出它的规则，得先看下面的情况

假设为 P：abcmcabcp 求它的 next 数组，一直求值到如下面的进度：

file

因为直到 r = 5 的时候 P[l] 才和 P[r] 相等，并且连续 3 次相等，所以直到 l=3，r=8 的时候 P[3] != P[8] 。此时的 next 数组为 [0, 0, 0, 0, 0, 1, 2, 3, 0]，注意，此时 next[8] 为 0 是因为还没有求的 next[8] 的值，默认值为 0。

P[3] != P[8]，说明 P[0..9] 没有最长相同前后缀子串，next[8] 所表示的要从哪个下标开始匹配的值，应该是什么呢？

因为我们要跳过尽可能多的重复字符，所以，当 P[3] != P[8] 的时候，我们要去看看它的前一个，P[7] 能够让我跳过几个字符

也就是求 P[0..8] 的最长相同前后缀子串的长度

也就是 next[7] 的值，抽象一下就是：next[r - 1] 的值 k

但是明明 k 是指最长相同前后缀子串的长度，为什么 k 可以直接被 P 当作下标使用呢？因为 k 也表示要跳过的长度，如果 k = 3，那么 跳过前 3 个，就是从第 4 个开始咯，第 4 个的下标表示形式就是 3 咯，因为下标从 0 开始的咯！

还记得刚才的 l = 0, r = 1 的情况吗，其实也适用于上面的规则，只不过因为 没有 0 - 1 的下标，所以当 P[l] != P[r] && l == 0 的时候，next[r] = 0

如果看不懂的话，多看几遍

构建 next 数组的代码如下：

function getNext(p) {
  let l = 0;
  let r = 1;
  let len = p.length;

  let n = [0];

  while (r < len) {
    if (p[l] === p[r]) {
      l++;
      r++;
      n.push(l);
    } else if (l > 0) {
      l = n[l - 1];
    } else {
      r++;
      n.push(0);
    }
  }

  return n;
}

构建 next 数组的时间复杂度为 O(n)

查找目标字符串

有了 next 数组，就可以在 S 中查找字符串了，逻辑也简单，S 和 P 的首位字符开始匹配，匹配相等就匹配两者的下一个字符，不相等就将 S 的当前匹配下标 i，作为 next 数组的下标，取得 k 值，S 的当前下标 j 不变，从 S[j] 和 P[k] 开始匹配。直到匹配完成或者失败

完整代码如下：

/**
 * @param {string} haystack
 * @param {string} needle
 * @return {number}
 */
var strStr = function (haystack, needle) {
  let next = getNext(needle);

  let hi = 0;
  let ni = 0;
  let len = haystack.length;

  while (hi < len) {
    if (haystack[hi] === needle[ni]) {
      hi++;
      ni++;
    } else if (ni > 0) {
      ni = next[ni - 1];
    } else {
      hi++;
    }

    if (ni === needle.length) {
      return hi - ni;
    }
  }

  return -1;
};

function getNext(p) {
  let l = 0;
  let r = 1;
  let len = p.length;

  let n = [0];

  while (r < len) {
    if (p[l] === p[r]) {
      l++;
      r++;
      n.push(l);
    } else if (l > 0) {
      l = n[l - 1];
    } else {
      r++;
      n.push(0);
    }
  }

  return n;
}